Matrices¶
- binomial
- cauchy
- chebspec
- chow
- circul
- clement
- companion
- dingdong
- fiedler
- forsythe
- frank
- golub
- grcar
- hadamard
- hankel
- hilb
- invhilb
- invol
- kahan
- kms
- lehmer
- lotkin
- magic
- minij
- moler
- neumann
- oscillate
- parter
- pascal
- pei
- poisson
- prolate
- randcorr
- rando
- randsvd
- rohess
- rosser
- sampling
- toeplitz
- tridiag
- triw
- vand
- wathen
- wilkinson
- binomial
A binomial matrix that arose from the example in [bmsz01]. The matrix is a multiple of involutory matrix.
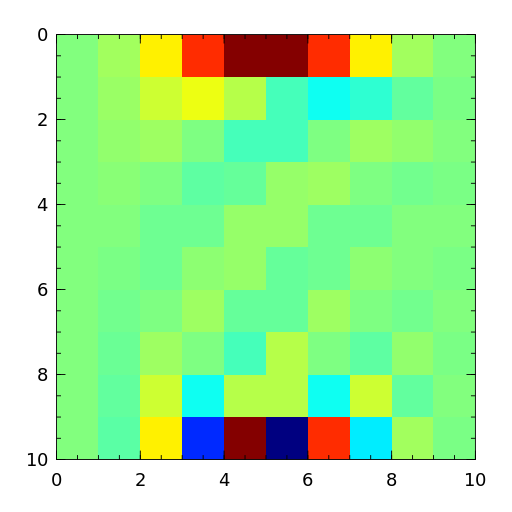
[bmsz01] G. Boyd, C.A. Micchelli, G. Strang and D.X. Zhou, Binomial matrices, Adv. in Comput. Math., 14 (2001), pp 379-391. - cauchy
The Cauchy matrix is an m-by-n matrix with \((i,j)\) element
\[\frac{1}{x_i - y_i}, \quad x_i - y_i \ne 0,\]where \(x_i\) and \(y_i\) are elements of vectors \(x\) and \(y\).
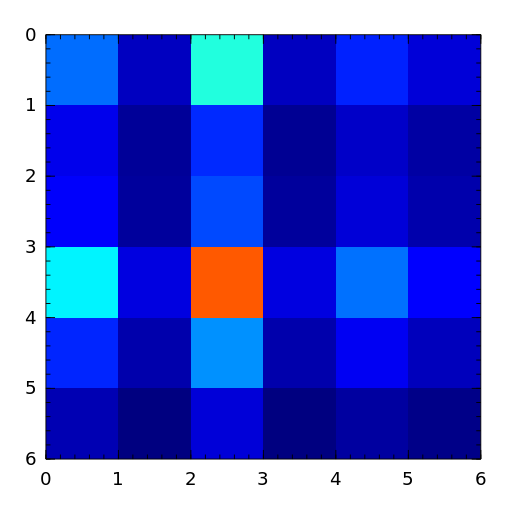
- chebspec
Chebyshev spectral differentiation matrix. If
k = 0,the generated matrix is nilpotent and a vector with all one entries is a null vector. Ifk = 1, the generated matrix is nonsingular and well-conditioned. Its eigenvalues have negative real parts.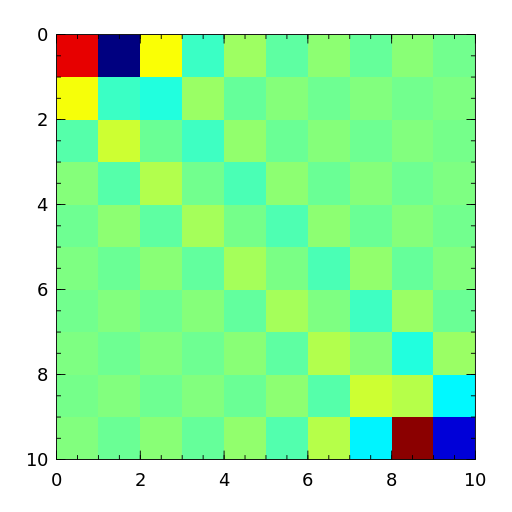
- chow
The Chow matrix is a singular Toeplitz lower Hessenberg matrix. The eigenvalues are known explicitly [chow69].
[chow69] T.S. Chow, A class of Hessenberg matrices with known eigenvalues and inverses, SIAM Review, 11 (1969), pp. 391-395. - circul
A circulant matrix has the property that each row is obtained by cyclically permuting the entries of the previous row one step forward.
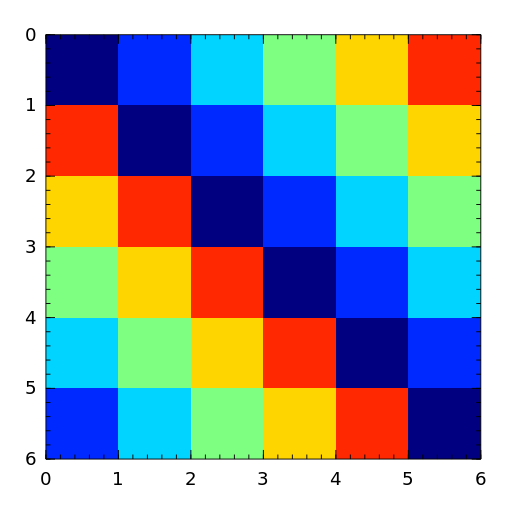
- clement
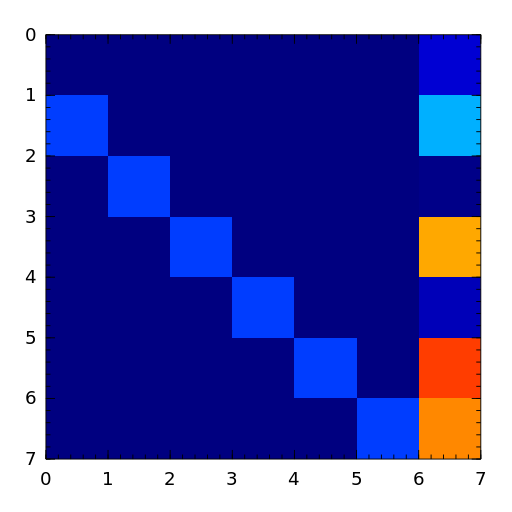
The Clement matrix [clem59] is a Tridiagonal matrix with zero diagonal entries. If
k = 1, the matrix is symmetric.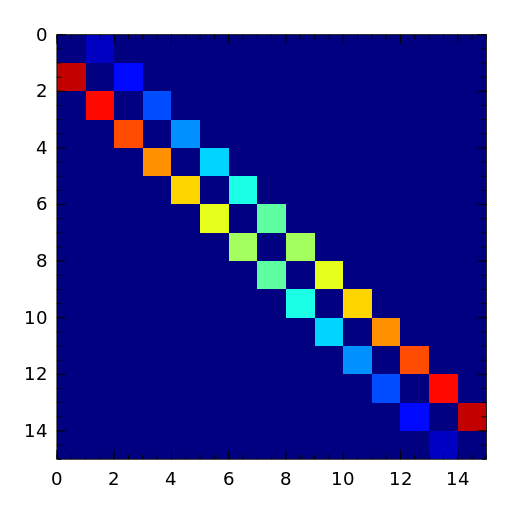
[clem59] P.A. Clement, A class of triple-diagonal matrices for test purposes, SIAM Review, 1 (1959), pp. 50-52. - companion
The companion matrix to a monic polynomial
\[a(x) = a_0 + a_1 x + \cdots + a_{n-1}x^{n-1} + x^n\]is the n-by-n matrix with ones on the subdiagonal and the last column given by the coefficients of a(x).
- dingdong
The Dingdong matrix is symmetric Hankel matrix invented by Dr. F. N. Ris of IBM, Thomas J Watson Research Centre. The eigenvalues cluster around \(\pi/2\) and \(-\pi/2\) [nash90].
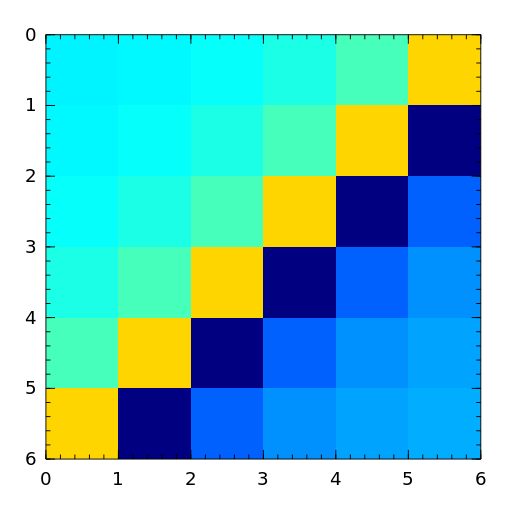
[nash90] J.C. Nash, Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation, second edition, Adam Hilger, Bristol, 1990 (Appendix 1). - fiedler
The Fiedler matrix is symmetric matrix with a dominant positive eigenvalue and all the other eigenvalues are negative. For explicit formulas for the inverse and determinant, see [todd77].
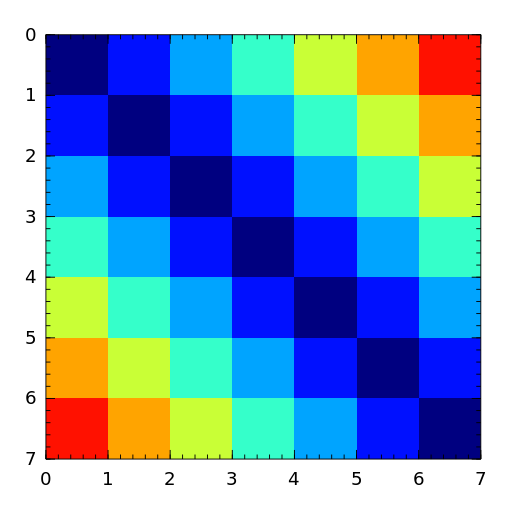
[todd77] J. Todd, Basic Numerical Mathematics, Vol. 2: Numerical Algebra, Birkhauser, Basel, and Academic Press, New York, 1977, pp. 159. - forsythe
The Forsythe matrix is a n-by-n perturbed Jordan block.
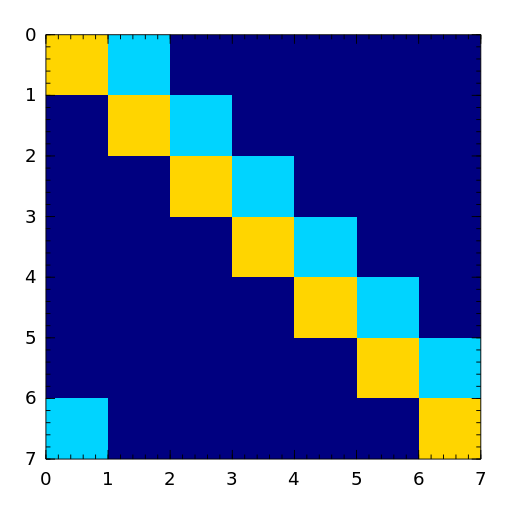
- frank
The Frank matrix is an upper Hessenberg matrix with determinant 1. The eigenvalues are real, positive and very ill conditioned [vara86].
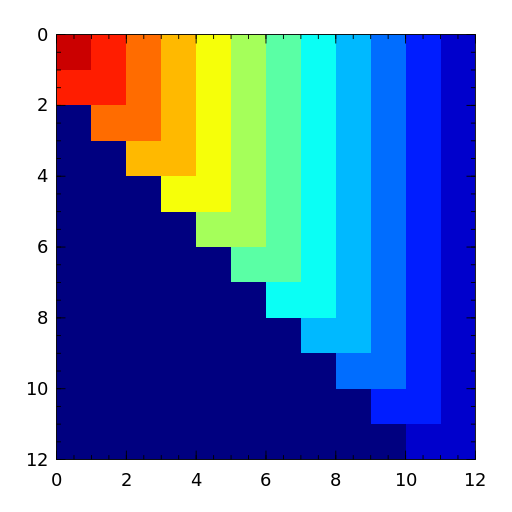
[vara86] J.M. Varah, A generalization of the Frank matrix, SIAM J. Sci. Stat. Comput., 7 (1986), pp. 835-839. - golub
Golub matrix is the product of two random unit lower and upper triangular matrices respectively. LU factorization without pivoting fails to reveal that such matrices are badly conditioned [vistre98].
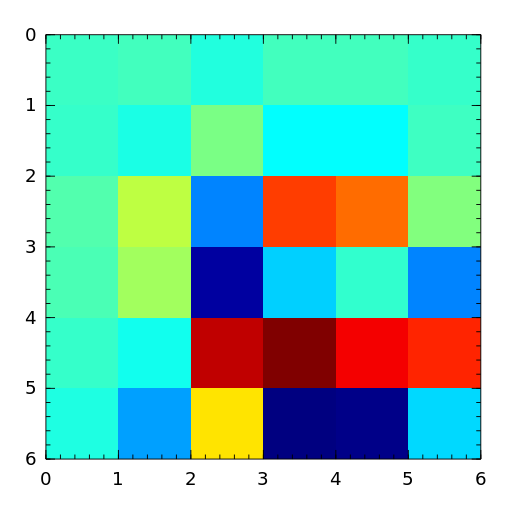
[vistre98] D. Viswanath and N. Trefethen. Condition Numbers of Random Triangular Matrices, SIAM J. Matrix Anal. Appl. 19, 564-581, 1998. - grcar
The Grcar matrix is a Toeplitz matrix with sensitive eigenvalues. The image below is a 200-by-200 Grcar matrix used in [nrt92].
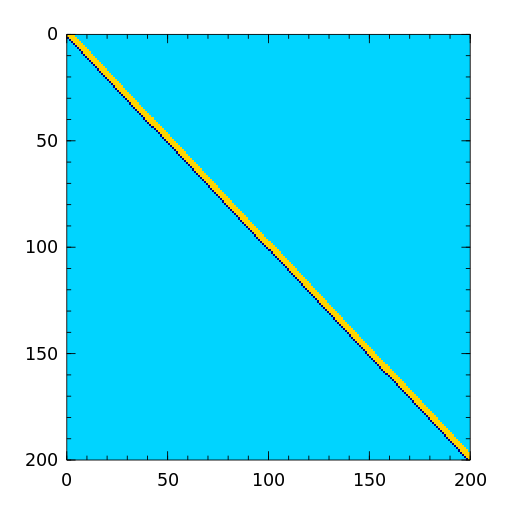
[nrt92] N.M. Nachtigal, L. Reichel and L.N. Trefethen, A hybrid GMRES algorithm for nonsymmetric linear system, SIAM J. Matrix Anal. Appl., 13 (1992), pp. 796-825. - hadamard
The Hadamard matrix is a square matrix whose entries are 1 or -1. It was named after Jacques Hadamard. The rows of a Hadamard matrix are orthogonal.
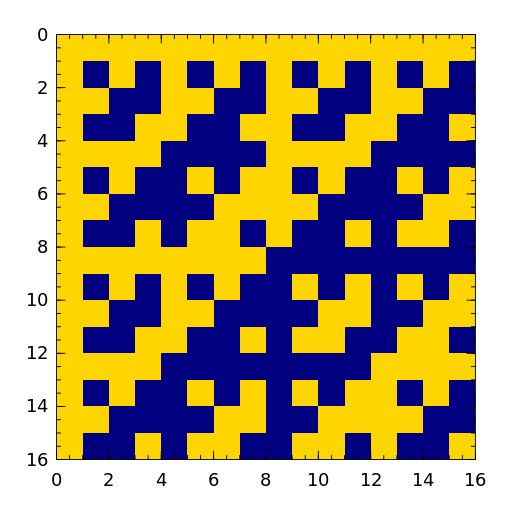
- hankel
Hankel matrix is a a matrix that is symmetric and constant across the anti-diagonals. For example:
julia> matrixdepot("hankel", [1,2,3,4], [7,8,9,10]) 4x4 Array{Float64,2}: 1.0 2.0 3.0 4.0 2.0 3.0 4.0 8.0 3.0 4.0 8.0 9.0 4.0 8.0 9.0 10.0
- hilb
The Hilbert matrix is a very ill conditioned matrix. But it is symmetric positive definite and totally positive so it is not a good test matrix for Gaussian elimination [high02] (Sec. 28.1).
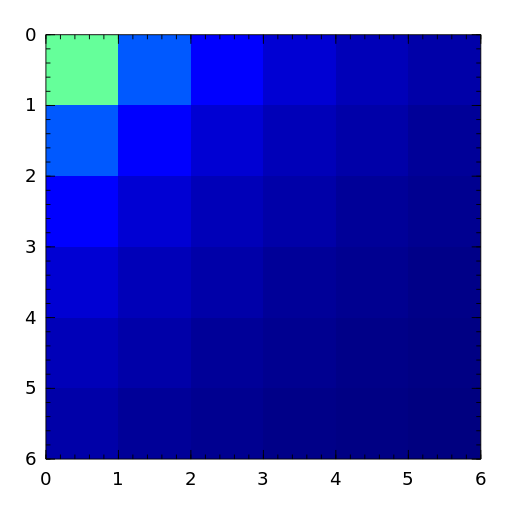
[high02] (1, 2, 3, 4) Nicholas J. Higham. Accuracy and Stability of Numerical Algorithms, SIAM, PA, USA. 2002. - invhilb
Inverse of the Hilbert Matrix.
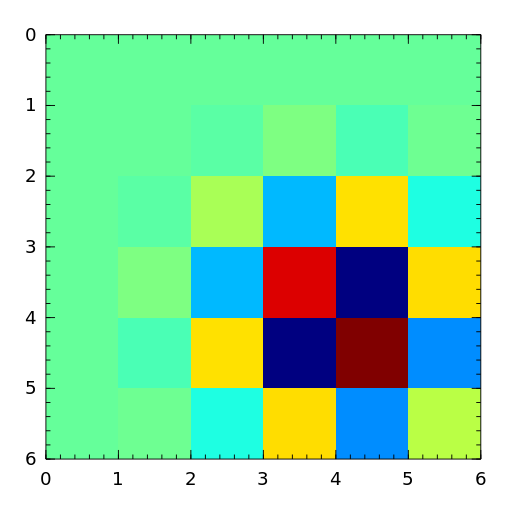
- invol
An involutory matrix, i.e., a matrix that is its own inverse. See [hoca63].
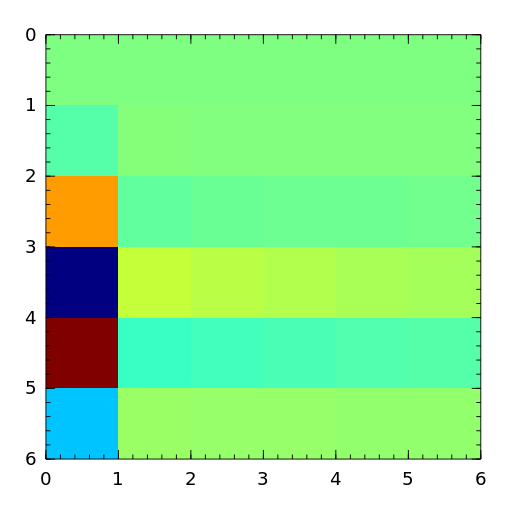
[hoca63] A.S. Householder and J.A. Carpenter, The singular values of involutory and idempotent matrices, Numer. Math. 5 (1963), pp. 234-237. - kahan
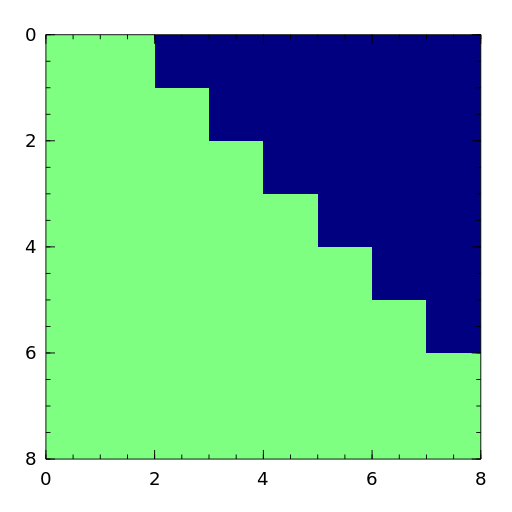
The Kahan matrix is a upper trapezoidal matrix, i.e., the \((i,j)\) element is equal to 0 if \(i > j\). The useful range of
thetais \(0 < theta < \pi\). The diagonal is perturbed bypert*eps()*diagm([n:-1:1]).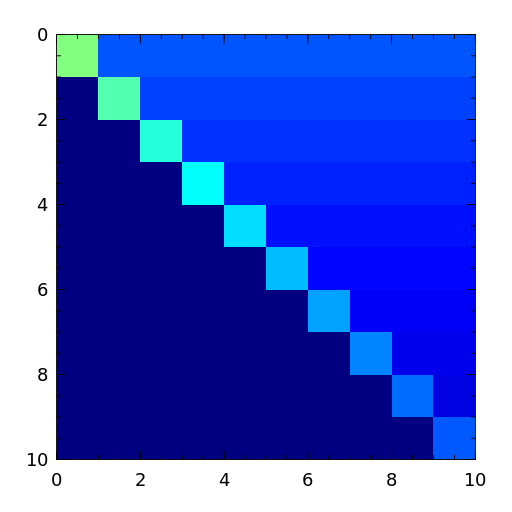
- kms
Kac-Murdock-Szego Toeplitz matrix [tren89].
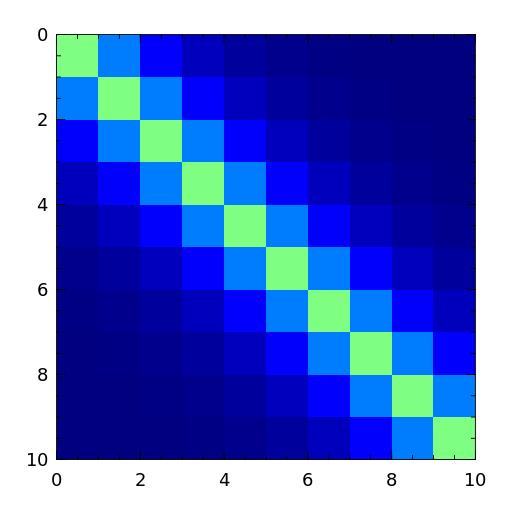
[tren89] W.F. Trench, Numerical solution of the eigenvalue problem for Hermitian Toeplitz matrices, SIAM J. Matrix Analysis and Appl., 10 (1989), pp. 135-146 - lehmer
The Lehmer matrix is a symmetric positive definite matrix. It is totally nonnegative. The inverse is tridiagonal and explicitly known [neto58].
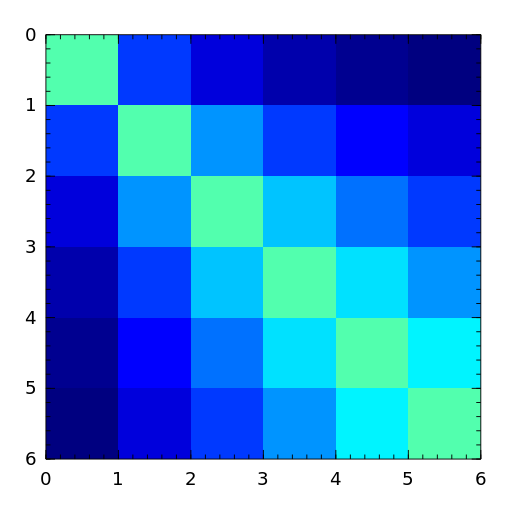
[neto58] M. Newman and J. Todd, The evaluation of matrix inversion programs, J. Soc. Indust. Appl. Math, 6 (1958), pp. 466-476. - lotkin
The Lotkin matrix is the Hilbert matrix with its first row altered to all ones. It is unsymmetric, ill-conditioned and has many negative eigenvalues of small magnitude [lotk55].
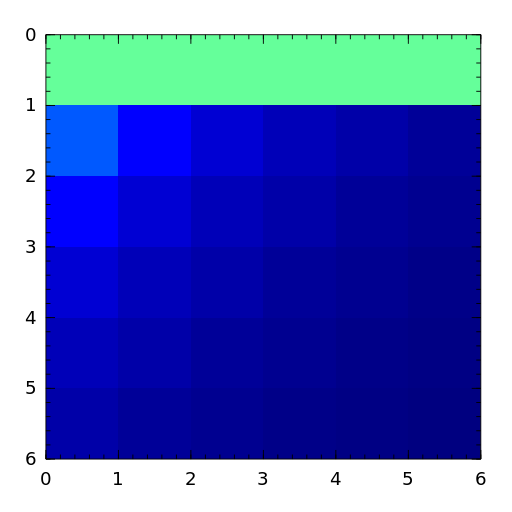
[lotk55] - Lotkin, A set of test matrices, MTAC, 9, (1955), pp. 153-161.
- magic
The magic matrix is a matrix with integer entries such that the row elements, column elements, diagonal elements and anti-diagonal elements all add up to the same number.
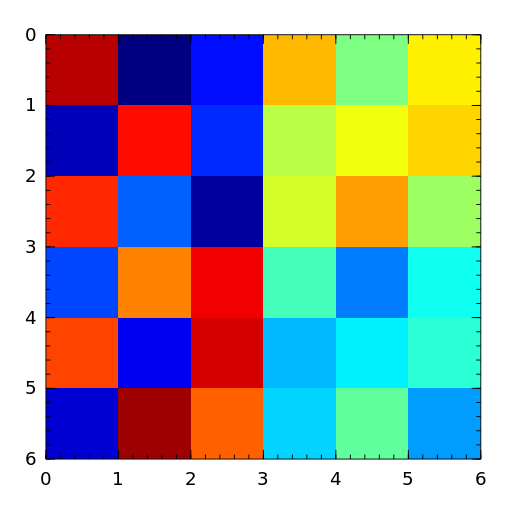
- minij
A matrix with \((i,j)\) entry
min(i,j). It is a symmetric positive definite matrix. The eigenvalues and eigenvectors are known explicitly. Its inverse is tridiagonal.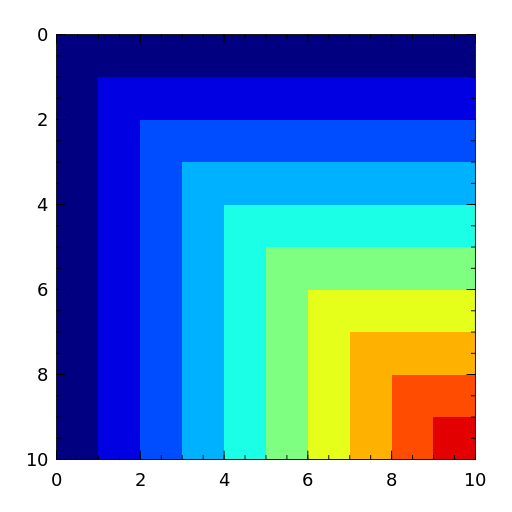
- moler
The Moler matrix is a symmetric positive definite matrix. It has one small eigenvalue.
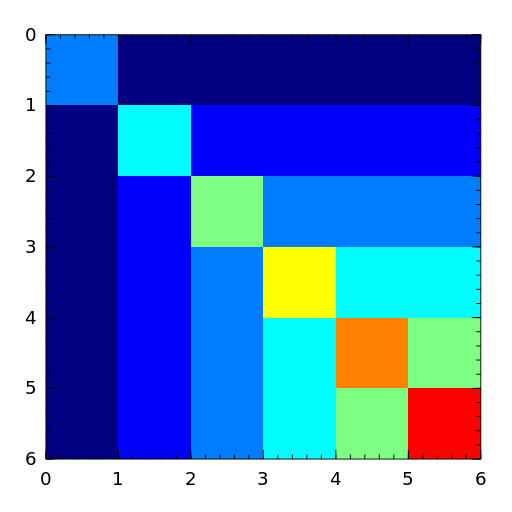
- neumann
A singular matrix from the discrete Neumann problem. This matrix is sparse and the null space is formed by a vector of ones [plem76].
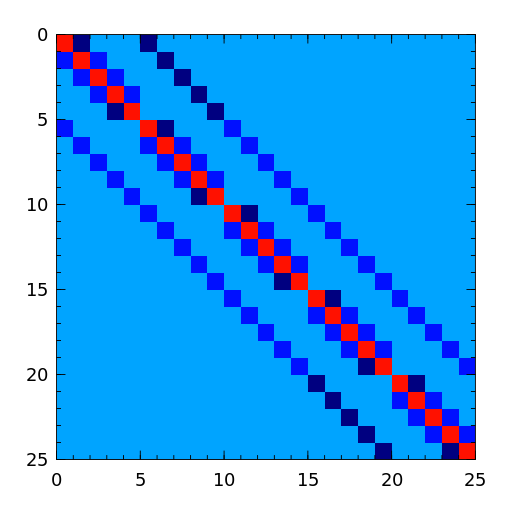
[plem76] R.J. Plemmons, Regular splittings and the discrete Neumann problem, Numer. Math., 25 (1976), pp. 153-161. - oscillate
A matrix \(A\) is called oscillating if \(A\) is totally nonnegative and if there exists an integer q > 0 such that A^q is totally positive. An \(n \times n\) oscillating matrix \(A\) satisfies:
- \(A\) has \(n\) distinct and positive eigenvalues \(\lambda_1 > \lambda_2 > \cdots > \lambda_n > 0\).
- The \(i\) th eigenvector, corresponding to \(\lambda_i\) in the above ordering, has exactly \(i -1\) sign changes.
This function generates a symmetric oscillating matrix, which is useful for testing numerical regularization methods [hansen95]. For example:
julia> A = matrixdepot("oscillate", 3) 3x3 Array{Float64,2}: 0.98694 0.112794 0.0128399 0.112794 0.0130088 0.0014935 0.0128399 0.0014935 0.00017282 julia> eig(A) ([1.4901161192617526e-8,0.00012207031249997533,0.9999999999999983], 3x3 Array{Float64,2}: 0.0119607 0.113658 -0.993448 -0.215799 -0.969813 -0.113552 0.976365 -0.215743 -0.0129276)
[hansen95] Per Christian Hansen, Test matrices for regularization methods. SIAM J. SCI. COMPUT Vol 16, No2, pp 506-512 (1995) - parter
The Parter matrix is a Toeplitz and Cauchy matrix with singular values near \(\pi\) [part86].
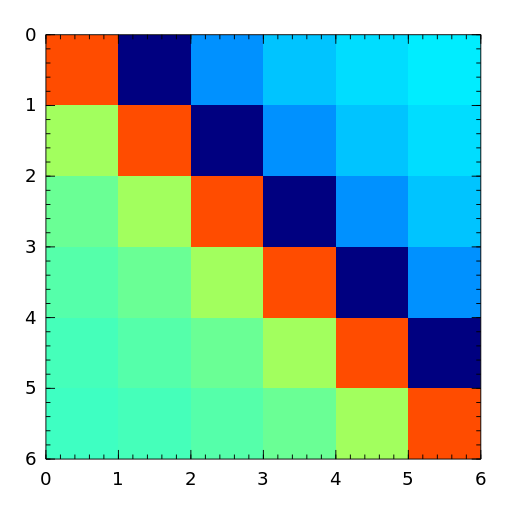
[part86] S. V. Parter, On the distribution of the singular values of Toeplitz matrices, Linear Algebra and Appl., 80 (1986), pp. 115-130. - pascal
The Pascal matrix’s anti-diagonals form the Pascal’s triangle:
julia> matrixdepot("pascal", 6) 6x6 Array{Int64,2}: 1 1 1 1 1 1 1 2 3 4 5 6 1 3 6 10 15 21 1 4 10 20 35 56 1 5 15 35 70 126 1 6 21 56 126 252
See [high02] (28.4).
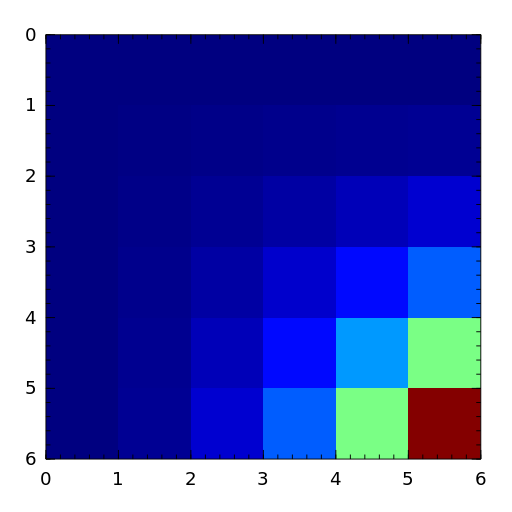
- pei
The Pei matrix is a symmetric matrix with known inverse [pei62].
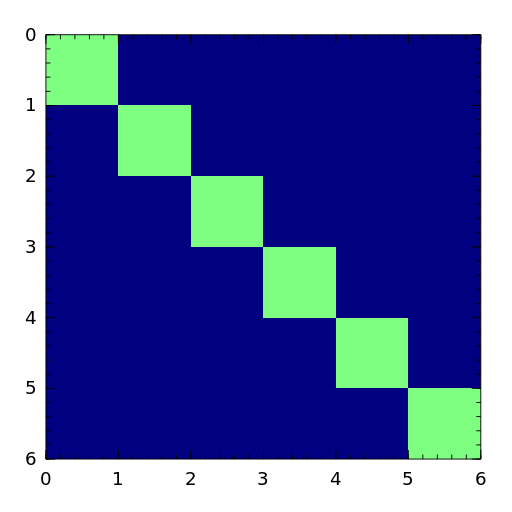
[pei62] M.L. Pei, A test matrix for inversion procedures, Comm. ACM, 5 (1962), pp. 508. - poisson
A block tridiagonal matrix from Poisson’s equation. This matrix is sparse, symmetric positive definite and has known eigenvalues.
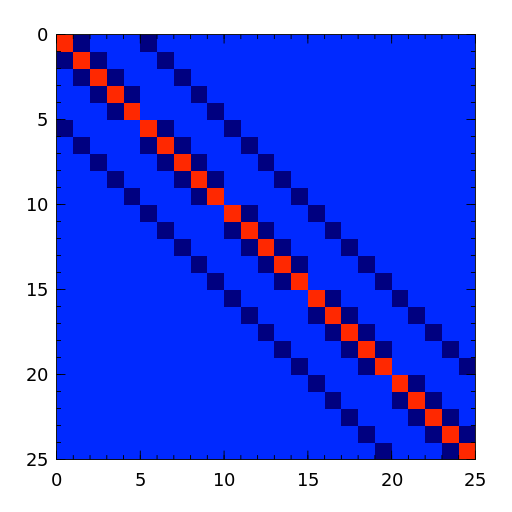
- prolate
A prolate matrix is a symmetric ill-conditioned Toeplitz matrix
\[\begin{split}A = \begin{bmatrix} a_0 & a_1 & \cdots \\ a_1 & a_0 & \cdots \\ \vdots & \vdots & \ddots \\ \end{bmatrix}\end{split}\]such that \(a_0= 2w\) and \(a_k = (\sin 2 \pi wk)/\pi k\) for \(k=1,2, \ldots\) and \(0<w<1/2\) [varah93].
[varah93] J.M. Varah. The Prolate Matrix. Linear Algebra and Appl. 187:267–278, 1993. - randcorr
A random correlation matrix is a symmetric positive semidefinite matrix with 1s on the diagonal.
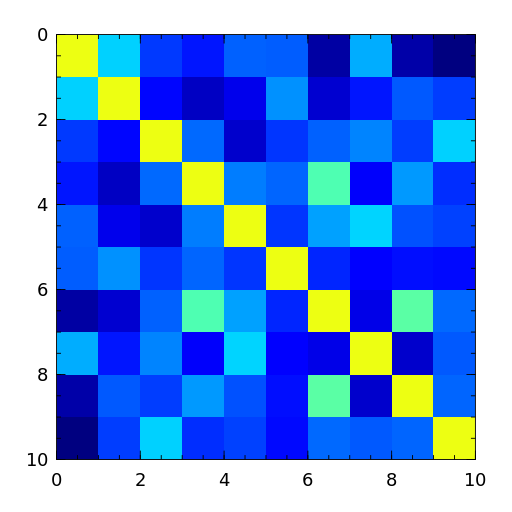
- rando
A random matrix with entries -1, 0 or 1.
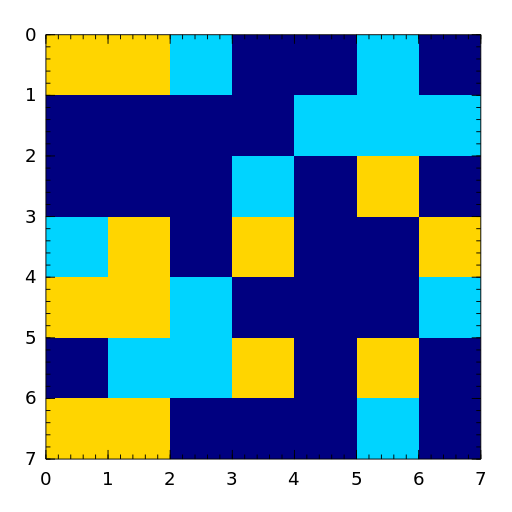
- randsvd
Random matrix with pre-assigned singular values. See [high02] (Sec. 28.3).
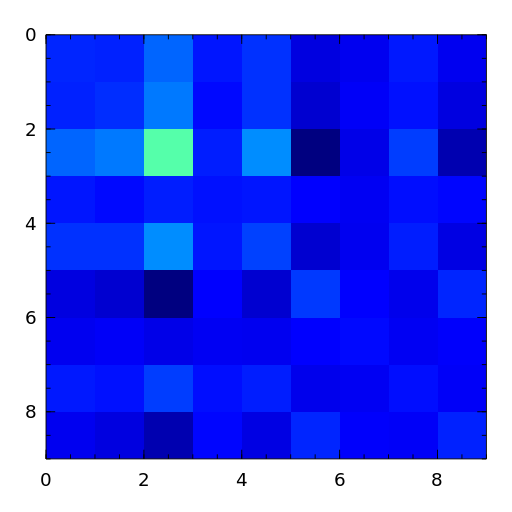
- rohess
A random orthogonal upper Hessenberg matrix. The matrix is constructed via a product of Givens rotations.
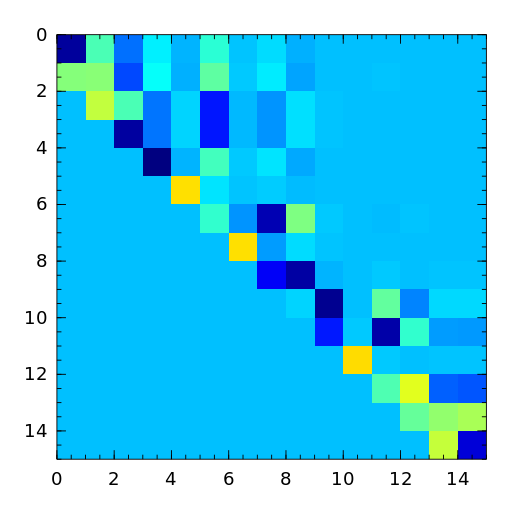
- rosser
The Rosser matrix’s eigenvalues are very close together so it is a challenging matrix for many eigenvalue algorithms.
matrixdepot("rosser", 8, 2, 1)generates the test matrix used in the paper [rlhk51].matrixdepot("rosser")are more general test matrices with similar property.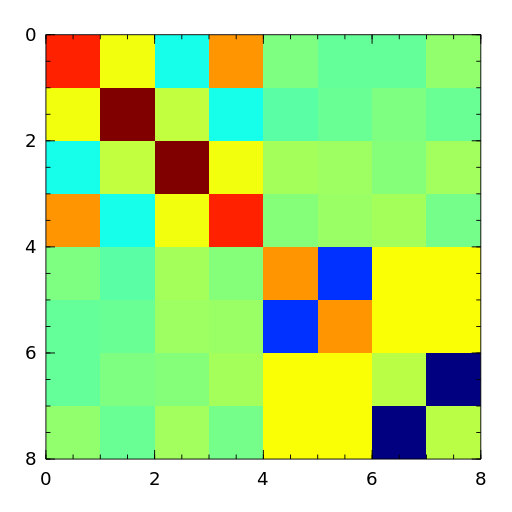
[rlhk51] Rosser, Lanczos, Hestenes and Karush, J. Res. Natl. Bur. Stand. Vol. 47 (1951), pp. 291-297. Archive - sampling
Matrices with application in sampling theory. A n-by-n nonsymmetric matrix with eigenvalues \(0, 1, 2, \ldots, n-1\) [botr07].
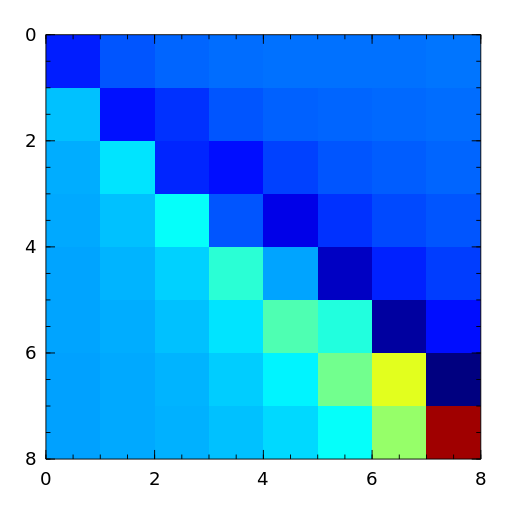
[botr07] L. Bondesson and I. Traat, A Nonsymmetric Matrix with Integer Eigenvalues, Linear and Multilinear Algebra, 55(3)(2007), pp. 239-247. - toeplitz
Toeplitz matrix is a matrix in which each descending diagonal from left to right is constant. For example:
julia> matrixdepot("toeplitz", [1,2,3,4], [1,4,5,6]) 4x4 Array{Int64,2}: 1 4 5 6 2 1 4 5 3 2 1 4 4 3 2 1 julia> matrixdepot("toeplitz", [1,2,3,4]) 4x4 Array{Int64,2}: 1 2 3 4 2 1 2 3 3 2 1 2 4 3 2 1
- tridiag
A group of tridiagonal matrices.
matrixdepot("tridiagonal", n)generate a tridiagonal matrix with 1 on the diagonal and -2 on the upper- lower- diagonal, which is a symmetric positive definite M-matrix. This matrix is also known as Strang’s matrix, named after Gilbert Strang.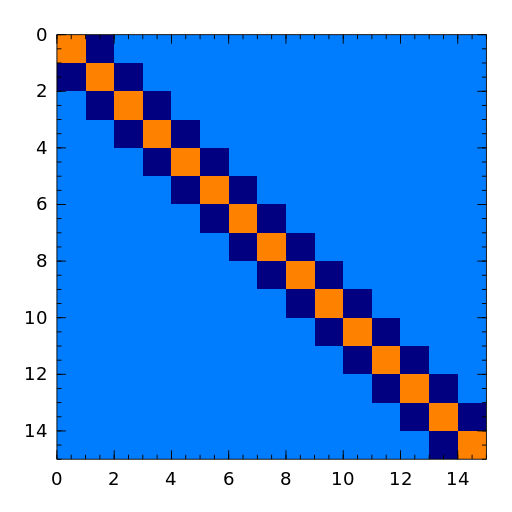
- triw
Upper triangular matrices discussed by Wilkinson and others [gowi76].
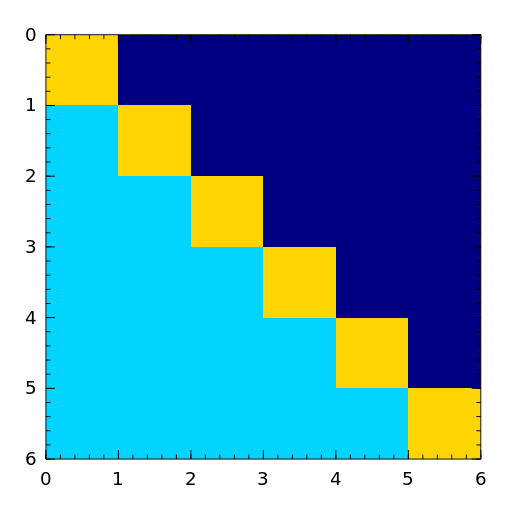
[gowi76] G.H. Golub and J.H. Wilkinson, Ill-conditioned eigensystems and the computation of the Jordan canonical form, SIAM Review, 18(4), (1976), pp. 578-619. - vand
The Vandermonde matrix is defined in terms of scalars \(\alpha_0, \alpha_1, \ldots, \alpha_n\) by
\[\begin{split}V(\alpha_0, \ldots, \alpha_n) = \begin{bmatrix} 1 & 1 & \cdots & 1 \\ \alpha_0 & \alpha_1 & \cdots & \alpha_n \\ \vdots & \vdots & & \vdots \\ \alpha_0^n & \alpha_1^n & \cdots & \alpha_n^n \\ \end{bmatrix}.\end{split}\]The inverse and determinant are known explicitly [high02].
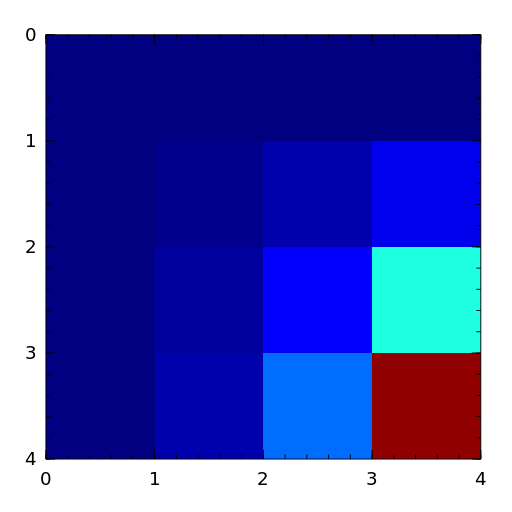
- wathen
The Wathen matrix is a sparse, symmetric positive, random matrix arising from the finite element method [wath87]. It is the consistent mass matrix for a regular nx-by-ny grid of 8-node elements.
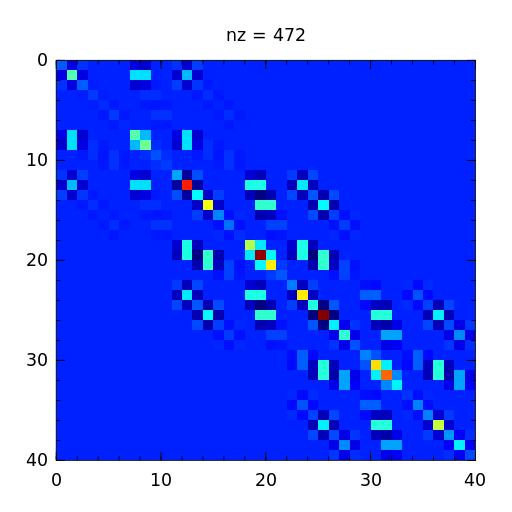
[wath87] A.J. Wathen, Realistic eigenvalue bounds for the Galerkin mass matrix, IMA J. Numer. Anal., 7 (1987), pp. 449-457. - wilkinson
The Wilkinson matrix is a symmetric tridiagonal matrix with pairs of nearly equal eigenvalues. The most frequently used case is
matrixdepot("wilkinson", 21).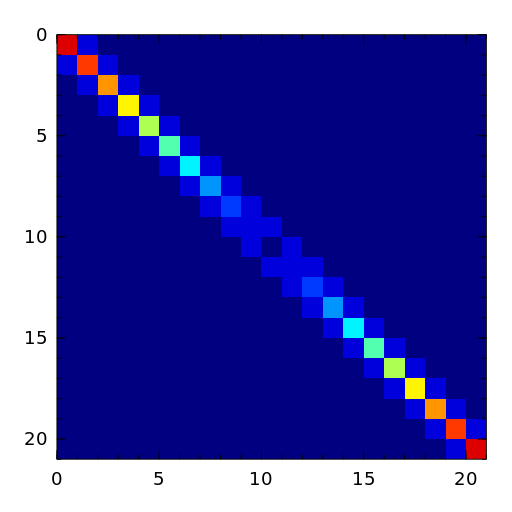
Note
The images are generated using Winston.jl
‘s imagesc function.